Modulo 5

modulo5

Argomenti

cenni di statistica descrittiva
caricamento e ispezione di dati in R
tipi di grafici di uso comune per la rappresentazione grafica di dati

Obiettivi conoscitivi

Al termine di questa attività dovresti essere in grado di:

scrivere comandi R per calcolare indicatori statistici descrittivi di variabili numeriche (media, mediana, deviazione standard)
scrivere comandi R per calcolare indicatori statistici descrittivi di variabili categoriche e logiche
scegliere un tipo di grafico adatto per visualizzare distribuzioni di variabili di interesse
scrivere comandi R per rappresentare graficamente una distribuzione di variabili (numeriche, logiche o categoriche)
caricare una tabella di dati di interesse dal proprio PC (esempio, da un file excel o testo semplice formattato in colonne)
elencare e descrivere almeno tre tipi di grafici di uso comune per rappresentare distribuzioni di variabili numeriche, logiche o categoriche

Durata e programma dell’attività:

4 ore;

[20']	Ricapitolando: vediamo insieme cosa abbiamo imparato a fare la volta scorsa
[50']	Statistica descrittiva: una panoramica introduttiva
pausa 5'
[30']	esercizi
pausa 15'
[40']	Slides statistica
[30']	Esercizi
pausa 10'
[20']	Spazio per domande e curiosità
[10']	Conclusioni

Ricapitolando: vediamo insieme cosa abbiamo imparato a fare la volta scorsa

Abbiamo conosciuto il quinto ed ultimo tipo di “oggetto” di R: la lista

r_liste

Abbiamo imparato come chiedere aiuto se abbiamo dubbi sul codice, in R o in rete

cmd

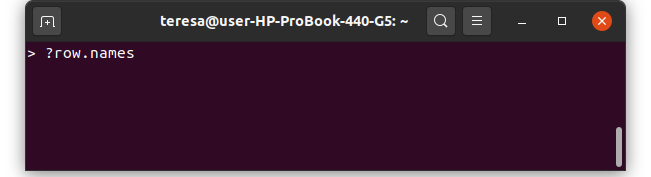
ad esempio dalla console di R, con il simbolo ? seguito dal nome della funzione per cui vogliamo vedere la documentazione

firefox

Oppure direttamente ad un motore di ricerca, per sapere come fare una certa cosa in R. Approfittando dei tanti utenti R e dei tanti forum con argomenti e problemi di ogni tipo già affrontati e risolti, e documentati in rete.

Abbiamo visto come installare e caricare nella propria sessione di lavoro un pacchetto R

cmd

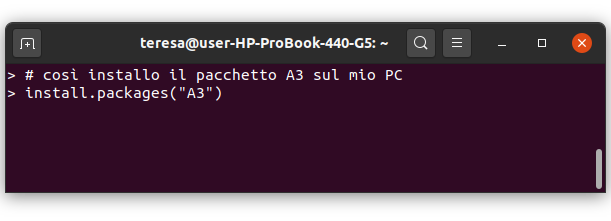
installo un pacchetto, dei tanti disponibili nel repository di R, una sola volta sul mio PC con la funzione install.packages()

cmd

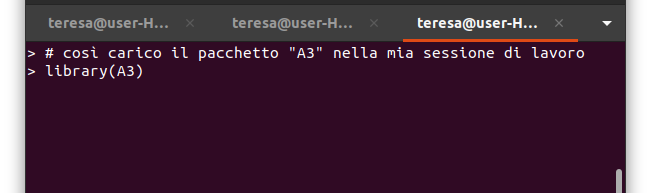
Ogni volta che voglio utilizzare funzioni da un dato pacchetto, carico quel pacchetto nella mia sessione di lavoro R con la funzione library()

Qua e là tra i capitoli abbiamo anche conosciuto

diversi altri esempi di funzioni disponibili in R, quali: list(), names(), sessionInfo()
un altro dei tanti dataset di esempio (in particolare, USArrests) già pronti da caricare nello spazio di lavoro di R per esercitarsi
abbiamo visto l’importanza delle parentesi: [], [[]], () … a proposito, sapresti dire ciascuno di questi tipi di parentesi quando si usa?

Statistica descrittiva: una panoramica introduttiva

La statistica descrittiva ha lo scopo di:

Riassumere i dati: Fornisce un quadro chiaro e sintetico di un insieme di dati.
Descrivere le caratteristiche principali: Aiuta a capire le caratteristiche essenziali dei dati, come la tendenza centrale e la variabilità.
Visualizzare i dati: Utilizza grafici e tabelle per rappresentare i dati in modo visivo e intuitivo.
Identificare pattern: Aiuta a individuare eventuali pattern, tendenze o anomalie nei dati.

In questa sezione, copriremo i seguenti argomenti:

Statistica descrittiva: scopi e modalità
Tipi di Variabili in Statistica
Distribuzioni di Frequenza Assolute e Relative
Principali Tipi di Grafico usati in Statistica Descrittiva
Indicatori Principali della Statistica Descrittiva
Importare Dati in R: Diversi Formati e Modi Possibili

Tipi di Variabili in Statistica

In statistica, le variabili si classificano in diversi tipi in base alla natura dei dati che rappresentano e al tipo di misurazione. Conoscere la tipologia di dati con cui si sta lavorando è essenziale per scegliere i giusti metodi di analisi statistica e per una corretta interpretazione dei risultati.Ecco una panoramica dei principali tipi di variabili:

1. Variabili Qualitative (o Categoriali)

Queste variabili descrivono categorie o attributi distinti e non numerici.

Nominali: Le categorie non hanno un ordine intrinseco. Esempi includono il colore degli occhi (blu, verde, marrone), il genere (maschio, femmina), e il tipo di veicolo (auto, moto, bici).
Ordinali: Le categorie hanno un ordine intrinseco, ma le distanze tra le categorie non sono misurabili. Esempi includono i livelli di istruzione (scuola elementare, media, superiore, università) e i livelli di soddisfazione (soddisfatto, neutro, insoddisfatto).

2. Variabili Quantitative (o Numeriche)

Queste variabili rappresentano quantità misurabili e possono essere numeri con significato matematico.

Discrete: Possono assumere solo valori distinti e separati (tipicamente numeri interi). Esempi includono il numero di figli in una famiglia, il numero di studenti in una classe, e il numero di macchine vendute.
Continue: Possono assumere qualsiasi valore in un intervallo continuo e possono essere frazionarie. Esempi includono l’altezza, il peso, e il tempo.

3. Variabili Dicotomiche e Logiche

Queste sono un tipo speciale di variabili nominali che hanno solo due categorie. Esempi includono il risultato di un test (passato/fallito) e la presenza o assenza di una caratteristica (sì/no). Un caso particolare di variabile dicotomica è rappresentato dalle variabili logiche (TRUE/FALSE). Queste ultime sono immediatamente interpretabili e trattabili come numeriche da R (1/0).

Principali Tipi di Grafico usati in Statistica Descrittiva

I grafici sono strumenti fondamentali per visualizzare i dati. La statistica descrittiva utilizza vari tipi di grafici per rappresentare visivamente i dati. Ogni tipo di grafico ha il suo specifico uso e può fornire diverse prospettive sui dati analizzati. Qui di seguito una panoramica dei principali tipi di grafico utilizzati nella statistica descrittiva con R. con esempi di codice R per ciascuno:

1. Istogramma

Un istogramma è utilizzato per rappresentare la distribuzione di una variabile numerica continua. Mostra la frequenza dei dati suddivisi in intervalli (bins).

# Genera un set di dati casuale
set.seed(123)	# questa funzione serve ad assicurare che tutti noi lavoreremo con gli stessi numeri (*)
data <- rnorm(100)

# Crea un istogramma
hist(data, main="Istogramma", xlab="Valori", ylab="Frequenza", col="blue", border="black")

(*) La funzione set.seed(), ad esempio set.seed(123), Imposta il seme del generatore di numeri casuali a 123. Questo significa che ogni volta che esegui il codice con lo stesso seme (123), otterrai la stessa sequenza di numeri casuali. Questo è particolarmente utile per garantire la riproducibilità dei risultati nelle analisi e nei test. Imposta il seme del generatore di numeri casuali a 123. Questo significa che ogni volta che esegui il codice con lo stesso seme (123), otterrai la stessa sequenza di numeri casuali. Questo è particolarmente utile per garantire la riproducibilità dei risultati nelle analisi e nei test.

2. Grafico a Barre (Barplot)

Un grafico a barre è utilizzato per rappresentare la frequenza o la percentuale di categorie di dati qualitativi.

# Genera dati categoriali
categories <- c("A", "B", "C", "D")
values <- c(10, 23, 15, 8)

# Crea un grafico a barre
barplot(values)

# Crea un grafico a barre un pò più informativo (aggiungendo i nomi alle categorie mostrate e agli assi)
barplot(values, names.arg=categories, main="Grafico a Barre", xlab="Categorie", ylab="Frequenza", col="lightblue")

3. Grafico a Scatola e Baffi (Boxplot)

Un boxplot è utilizzato per visualizzare la distribuzione di una variabile numerica continua attraverso i suoi quartili. È utile per identificare i valori anomali. In particolare, in un boxplot vengono evidenziate i seguenti cinque indicatori statistici:

Minimo (Minimum): cioé il valore più piccolo nel dataset, esclusi gli outlier. Rappresentato dalla linea inferiore (baffo) che si estende dalla scatola.
Primo Quartile (Q1): cioé il 25° percentile dei dati, il valore sotto il quale cade il 25% dei dati. Rappresenta il bordo inferiore della scatola.
Mediana (Median): cioé il valore centrale dei dati, il 50° percentile. Indica che il 50% dei dati è inferiore a questo valore e il 50% è superiore. Rappresentata dalla linea all’interno della scatola.
Terzo Quartile (Q3): cioé il 75° percentile dei dati, il valore sotto il quale cade il 75% dei dati. Rappresenta il bordo superiore della scatola.
Massimo (Maximum): cioé il valore più grande nel dataset, esclusi gli outlier. Rappresentato dalla linea superiore (baffo) che si estende dalla scatola.

Inoltre, i Baffi (Whiskers), di un boxplot, cioé Le linee che si estendono dalla scatola ai valori minimi e massimi (esclusi gli outlier), raccontano la dispersione dei dati al di fuori del primo e del terzo quartile. Avendo questi riferimenti statistici, chiameremo outlier:, cioé valori anomali o estremi della nostra distribuzione di dati, quei i punti dati che si trovano al di fuori dei baffi. Infatti, gli outlier sono solitamente definiti come punti che si trovano oltre 1.5 volte l’intervallo interquartile (IQR, dall’inglese InterQuartile Range). Quindi oltre i valori dati da: (Q1 - 1.5IQR) e (Q3 + 1.5IQR).

# Genera un set di dati casuale
set.seed(123)
data <- rnorm(100)

# Crea un boxplot
boxplot(data, main="Boxplot", ylab="Valori", col="lightgreen")

4. Grafico a Dispersione (Scatter Plot)

Un grafico a dispersione è utilizzato per visualizzare la relazione tra due variabili numeriche.

# Genera due set di dati correlati
set.seed(123)
x <- rnorm(100)
y <- 2 * x + rnorm(100)

# Crea un grafico a dispersione
plot(x, y, main="Grafico a Dispersione", xlab="Variabile X", ylab="Variabile Y", col="red", pch=19)

5. Grafico a Torta

Un grafico a torta è utilizzato per rappresentare la proporzione di diverse categorie di dati qualitativi.

# Genera dati categoriali
slices <- c(10, 23, 15, 8)
labels <- c("A", "B", "C", "D")

# Crea un grafico a torta
pie(slices, labels=labels, main="Grafico a Torta", col=rainbow(length(slices)))

Distribuzione di Frequenza

La distribuzione di frequenza mostra come i dati sono distribuiti tra diverse categorie o intervalli.

# Genera un set di dati
data <- c(18 ,19 , 20 , 30 , 29 , 28 , 21 , 22 , 23 , 27 , 26 , 25 , 24 , 25 , 26, 24 , 23 , 22 , 27 , 28 , 21 , 24 , 25 , 25 , 27 , 19 , 21 , 28 , 29, 28)

# Calcola la distribuzione di frequenza
frequency_distribution <- table(data)
print(frequency_distribution)
# Output:
# data
# 18 19 20 21 22 23 24 25 26 27 28 29 30 
# 1  2  1  3  2  2  3  4  2  3  4  2  1 

Una funzione di R utile per un riepilogo dei dati: summary()

La funzione summary() in R è uno strumento potente e versatile che fornisce un riepilogo statistico dei principali indicatori di un set di dati. È particolarmente utile per ottenere rapidamente una panoramica delle caratteristiche di un dataset e per individuare eventuali valori anomali o pattern interessanti.

Cosa Fa summary()

Quando si applica la funzione summary() a un dataset, essa restituisce i seguenti indicatori statistici per ciascuna variabile:

Valore Minimo (Min.): Il valore più basso nel dataset.
Primo Quartile (1st Qu.): Il valore al 25-esimo percentile.
Mediana (Median): Il valore al 50-esimo percentile.
Media (Mean): La media aritmetica dei valori.
Terzo Quartile (3rd Qu.): Il valore al 75-esimo percentile.
Valore Massimo (Max.): Il valore più alto nel dataset.

Per le variabili categoriche, summary() restituisce un conteggio delle occorrenze di ciascun livello, che mi consente di:

avere una panoramica dei dati: Fornisce un riepilogo conciso delle principali statistiche descrittive.
identificare eventuali outliers: Facilita l’individuazione di valori anomali.
verifica l’eventuale presenza di dati mancanti: Indica la presenza di valori mancanti (NAs).

Di sequito un esempio di utilizzo della funzione summary() con un semplice dataset:

# Creazione di un dataset di esempio
data <- data.frame(
  age = c(23, 25, 31, 35, 42, 58, 60, 22, 30, 40),
  salary = c(50000, 60000, 80000, 55000, 120000, 70000, 75000, 65000, 62000, 58000)
)

# Applicazione della funzione summary()
summary_stats <- summary(data)
print(summary_stats)

Distribuzioni di Frequenza Assolute e Relative

Distribuzione di Frequenza Assoluta
La distribuzione di frequenza assoluta è una tabulazione che mostra il numero di occorrenze di ciascun valore o intervallo di valori in un dataset. È utile per capire come i dati sono distribuiti in termini di conteggio.

Distribuzione di Frequenza Relativa
La distribuzione di frequenza relativa, invece, esprime la frequenza assoluta come una frazione o una percentuale del totale. È utile per confrontare distribuzioni di dataset di dimensioni diverse, poiché normalizza i dati rispetto al totale.

Utilità

Comprensione della Distribuzione dei Dati: Permette di visualizzare come i dati sono distribuiti e individuare pattern o anomalie.
Confronto di Dataset: Le frequenze relative facilitano il confronto tra dataset di dimensioni diverse.
Base per Altre Analisi: Costituiscono il punto di partenza per calcolare ulteriori statistiche descrittive o per visualizzazioni grafiche come istogrammi.

Un paio di funzioni di R utile per calcolare frequenze assolute e relative: table() e prop.table()

Ecco un esempio di come calcolare e visualizzare le distribuzioni di frequenza assolute e relative in R:

# Creazione di un dataset di esempio
data <- c(2, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 7)

# Calcolo della distribuzione di frequenza assoluta
freq_abs <- table(data)
print(freq_abs)

# Calcolo della distribuzione di frequenza relativa
freq_rel <- prop.table(freq_abs)
print(freq_rel)

Indicatori Principali della Statistica Descrittiva (parte A: Misure di tendenza centrale)

Queste misure indicano il valore centrale o tipico di un insieme di dati.

La statistica descrittiva si avvale di diversi indicatori per riassumere e descrivere le caratteristiche principali di un insieme di dati. Ecco una panoramica degli indicatori più comuni e degli esempi su come calcolarli in R.

1. Media

La media aritmetica è la somma di tutti i valori divisa per il numero di valori. È un indicatore della tendenza centrale dei dati.

# Genera un set di dati
data <- c(2, 4, 6, 8, 10)

# Calcola la media
mean_value <- mean(data)
print(mean_value)  # Output: 6

2. Mediana

La mediana è il valore che separa la metà superiore dei dati dalla metà inferiore. È meno sensibile ai valori anomali rispetto alla media.

# Genera un set di dati
data <- c(2, 4, 6, 8, 10)

# Calcola la mediana
median_value <- median(data)
print(median_value)  # Output: 6

3. Moda

La moda è il valore che appare più frequentemente nei dati.
Nota: in R, non esiste una funzione predefinita per calcolare la moda, ma puoi facilmente scrivere un piccolo codice R personalizzato per farlo. Ecco come puoi calcolare la moda di un vettore di dati:

# Genera un set di dati
data <- c(2, 4, 6, 8, 10, 10, 5, 8, 9, 8)

# Passaggi per calcolare la moda

# 1. usa la funzione **table()** per contare la frequenza di ogni valore
frequenze <- table(data)

# 2. Trova il valore con la frequenza massima
moda <- as.numeric(names(frequenze)[frequenze == max(frequenze)])
print(moda)  # Output: 8

Indicatori Principali della Statistica Descrittiva (parte B: Misure di dispersione dei dati)

Queste misure indicano il valore centrale o tipico di un insieme di dati.

1. Deviazione Standard

La deviazione standard misura la dispersione dei dati rispetto alla media. Infatti indica quanto i valori si discostano in media dalla media. Un valore elevato indica che i dati sono molto dispersi.

# Genera un set di dati
data <- c(2, 4, 6, 8, 10)

# Calcola la deviazione standard
sd_value <- sd(data)

# Stampa il valore della deviazione standard
print(sd_value)

2. Varianza

La varianza rappresenta la media dei quadrati delle differenze tra ciascun valore e la media.

# Genera un set di dati
data <- c(2, 4, 6, 8, 10)

# Calcola la varianza
variance_value <- var(data)

# Stampa il valore della varianza
print(variance_value)

3. Range

Il range (o intervallo) è la misura della differenza tra il valore massimo e il valore minimo di una serie di numeri. Può essere influenzato dalla presenza di outlier.

# Genera un set di dati
data <- c(2, 4, 6, 8, 10)

# Calcola il range
range_value <- range(data)

# Calcola la differenza tra il massimo e il minimo per ottenere il range
range_difference <- diff(range_value)

# Stampa il range
print(range_difference)

Esercizio guidato: Calcolo della Media, Mediana e Deviazione Standard

Esegui il codice riportato nel seguente esercizio utilizzando R sul tuo PC.

# Crea un vettore numerico
data <- c(4, 8, 6, 5, 3, 8, 9, 7, 6, 8)

# Calcola la media
media <- mean(data)
cat("Media:", media, "\n")

# Calcola la mediana
mediana <- median(data)
cat("Mediana:", mediana, "\n")

# Calcola la deviazione standard
sd <- sd(data)
cat("Deviazione standard:", sd(data), "\n")

Mettiti alla prova!

Ora prova tu a scrivere un codice che faccia quanto indicato nei commenti qui sotto. Immagina di avere i punteggi degli studenti in un esame e di volerne trarre una descrizione statistica. Per farlo, fai riferimento ai blocchi di codice R visti qui sopra.

# Utilizza il seguente vettore di dati per svolgere l'esercizio:
voti <- c(18 , 25 , 23 , 28 , 24 , 26 , 19 , 30 , 25 , 27 , 23 , 26 , 25 , 19 , 20)

# Calcola la media dei voti

# Calcola la mediana dei voti

# Trova la moda per capire qual'è il voto preso più frequente (qual'è il voto preso più di frequente?)

# Calcola la deviazione standard per vedere quanto variano i voti rispetto alla media

# Crea un boxplot per visualizzare la distribuzione dei voti

Importare Dati in R: Diversi Formati e Modi Possibili

R offre diverse funzioni per importare dati da vari formati di file. Di seguito vengono illustrati i modi più comuni per leggere tabelle di dati in R, con esempi di codice per ciascun formato.

Importare Dati da un File CSV

Il formato CSV (Comma-Separated Values) è uno dei formati più comuni per l’archiviazione e lo scambio di dati tabulari. In R, si utilizza la funzione read.csv().

Per un file CSV da usare come esempio, scarica questo file (“anagrafica-vaccini-summary-latest.csv”) sul tuo PC che riporta i dati del Ministero della Salute sui vaccinati in Italia.

# Importare dati da un file CSV
data_csv <- read.csv("path/to/yourfile.csv")	# adatta questo comando con il path sul tuo PC al file "anagrafica-vaccini-summary-latest.csv" appena scaricato
head(data_csv)

Importare Dati da un File TSV Il formato TSV (Tab-Separated Values) utilizza il tab come delimitatore. In R, si può usare la funzione read.table() specificando che il delimitatore è la tabulazione (argomento sep=”\t”).

# Importare dati da un file TSV
data_tsv <- read.table("path/to/yourfile.tsv", sep="\t", header=TRUE)
head(data_tsv)

Importare Dati da un File di Testo con Delimitatore Personalizzato Se si ha un file di testo con un delimitatore diverso da virgola o tab, si può di nuovo utilizzare la funzione generica read.table(), specificando il delimitatore corretto come valore dell’argomento sep. Esempio: read.table(miofile, sep=”;”), per importare una tabella di dati i cui valori sono separati da un “;”.

# Importare dati da un file di testo con delimitatore personalizzato
data_custom <- read.table("path/to/yourfile.txt", sep=";", header=TRUE)
head(data_custom)

Importare Dati da un File Excel Per leggere file Excel (.xls o .xlsx), si può utilizzare il pacchetto readxl.
Per un file excel da usare come esempio, scarica questo file (“lhfa_girls_0-to-13-weeks_zscores.xlsx”) sul tuo PC che riporta i dati della World Health Organization (WHO) su peso e altezza di bambine tra 0 e 13 settimane.

# Installare e caricare il pacchetto readxl
# install.packages("readxl") # decommenta ed esegui questo comando se hai bisogno di installare il pacchetto "readxl"
library(readxl)

# Importare dati da un file Excel
data_excel <- read_excel("path/to/yourfile.xlsx", sheet = 1)	# es. adatta con il path al file "lhfa_girls_0-to-13-weeks_zscores.xlsx"
head(data_excel)

Importare Dati da una Connessione URL È possibile importare dati direttamente da una URL che punta a un file CSV.

# Importare dati da una URL
url <- "https://raw.githubusercontent.com/italia/covid19-opendata-vaccini/master/dati/anagrafica-vaccini-summary-latest.csv"
data_url <- read.csv(url)
head(data_url)

Un excursus: file excel. Quando è una tabella e… quando è arte

Attenzione all’uso creativo dello spazio nei fogli excel. Spesso per armonia di visione “umana”, si dispongono dati in un foglio excel perdendo completamente il formato righe e colonne che caratterizza una matrice di dati. E che è anche l’unico formato (righe x colonne) importabile in R.
Prova ad esempio a scaricare(*) i seguenti file EXCEL sul tuo PC. Aprili e prova a capire cosa NON va:
Esempio 1 Esempio 2

(*) Nella pagina che si aprirà, per scaricare il file EXCEl premi l’icona di download presente tutto a destra nella banda grigia.

Vediamo un esempio di analisi descrittiva utilizzando il dataset iris in R:

Il dataset iris è un esempio di dataset già caricato e disponibile come data.frame in R. Contiene misurazioni di quattro caratteristiche (lunghezza e larghezza sia dei sepali che dei petali) di tre diverse specie di fiori di iris. Si deve a Ronald A. Fisher, che nel 1936 lo ha creato come parte del suo lavoro sulla discriminazione lineare. Ecco i dettagli del dataset:

Dimensioni:

150 osservazioni (righe)
5 variabili (colonne)

Variabili:

Sepal.Length: Lunghezza del sepalo (in centimetri).
Sepal.Width: Larghezza del sepalo (in centimetri).
Petal.Length: Lunghezza del petalo (in centimetri).
Petal.Width: Larghezza del petalo (in centimetri).
Species: Specie del fiore di iris, con tre possibili valori: setosa, versicolor o virginica

# Caricamento del dataset
data(iris)

# Riepilogo statistico
summary(iris)

# Media e deviazione standard
mean(iris$Sepal.Length)
sd(iris$Sepal.Length)

# Varianza
var(iris$Sepal.Length)

# suddividiamo il dataset iris in 3 diversi subset, uno per ogni specie
iris_setosa <- subset(iris,Species == "setosa" )
iris_versicolor <- subset(iris,Species == "versicolor" )
iris_virginica <- subset(iris,Species == "virginica" )

#.... **per te**: prova ad usare la funzione **dim()** per scoprire le dimensioni di ciascuno di questi 3 subset di dati appena generati.

# Istogramma: visualizziamo la distribuzione di lunghezza dei sepali tra tutte le specis di iris considerate
hist(iris$Sepal.Length, main="Istogramma di Sepal Length", xlab="Lunghezza del sepalo", col="cyan")

# ora calcoliamo le medie di lunghezza dei sepali per ogni diversa specie di iris, e aggiungiamo questa informazione come barre verticali nell'istogramma appena creato
mean.sepal.len_setosa <- mean(iris_setosa$Sepal.Length)
mean.sepal.len_versicolor <- mean(iris_versicolor$Sepal.Length)
mean.sepal.len_virginica <- mean(iris_virginica$Sepal.Length)

abline( v=mean.sepal.len_setosa, lty=2, col="blue", lwd=1.5)	# la funzione **abline()** aggiunge una linea verticale o orizzontale nella posizione specificata dal parametro v oppure h, rispettivamente.
abline( v=mean.sepal.len_versicolor, lty=2, col="red", lwd=1.5)	# con il parametro **lwd=1.5** sto aumentando lo spessore della linea (line width) per renderlo più evidente rispetto al valore 1 (default).
abline( v=mean.sepal.len_virginica, lty=2, col="green", lwd=1.5)

# aggiungiamo una legenda che specifichi cosa rappresentano le linee verticali
legend("topright", lty=2, lwd=2, col=c("blue","red","green"), legend=c("setosa","versicolor","virginica"))

#.... **per te**: ti aiuta questa rappresentazione grafica dei dati a individuare pattern interessanti?


# Boxplot: confrontiamo in altro modo le distribuzioni di lunghezza dei sepali tra le diverse specie
boxplot(iris$Sepal.Length ~ iris$Species, main="Boxplot di Sepal Length per Specie", xlab="Specie",
	ylab="Lunghezza del sepalo", col=c("blue","red","green"), legend=TRUE)


# Scatter plot: altro scopo nella statistica descrittiva è evidenziare possibili associazioni tra variabili.
# Lo scatter plot è una rappresentazione grafica utile a identificare possibili associazioni tra i variabili.

plot(iris$Sepal.Length, iris$Petal.Length, main="Scatter plot di Sepal Length vs Petal Length", xlab="Lunghezza del sepalo", ylab="Lunghezza del petalo", col="red")

# aggiungiamo al plot i punti, in diversi colori, relativi alle singole specie utilizzando la funzione **points()**
points(iris_setosa$Sepal.Length, iris_setosa$Petal.Length, col="blue", pch=16)	# con pch=1 usiamo il pallino pieno per maggior evidenza
points(iris_versicolor$Sepal.Length, iris_versicolor$Petal.Length, col="red", pch=16)

#.... **per te**: aggiungi un'altra riga di codice per visualizzare nel plot anche i punti relativi alla specie virginica, in colore verde ("green")

# proviamo a "fittare" un modello di regressione lineare per evidenziare la dipendenza tra lunghezza del sepalo e del petalo che sembra emergere dal plot
<br>
# a questo scopo, utilizzaiamo la funzione **lm()**
lm(Sepal.Length ~ Petal.Length, data=iris) 	# con questo comando stimiamo x e y della retta di minimizazione delle distanze che vogliamo stimare
abline( lm(Sepal.Length ~ Petal.Length, data=iris) ) 	# con questo comando aggiungiamo la retta appena stiata dal modello nel plot




# aggiungiamo una legenda in alto a sinistra
legend("topleft", pch=16, col=c("blue","red"), legend=c("setosa","versicolor"))

#.... **per te**: modifica il comando qui sopra affinché nella legenda compaia anche la specie "virginica". Poi rigenera da capo il plot,
#	con questa legenda completa in sostituzione di quella parziale generata dal comando qui sopra

#.... **per te**: come puoi scoprire tutta la gamma di valori del parametro pch (cioé, aspetto del punto sul plot) a tua disposizione in R?



# matematicamente, l'associazione tra due variabili può essere saggiata valutandone la correlazione. Ad esempio, utilizzando la funzione **cor()**
cor(iris$Sepal.Length, iris$Petal.Length)

#.... **per te**: ti sembra ci sia evidenza di una qualche associazione tra lunghezza dei sepali e dei petali nelle varie specie?

Vediamo un altro esempio di analisi descrittiva, utilizzando un dataset di altezze di studenti:

In questo esempio, esamineremo un dataset di altezze degli studenti utilizzando la statistica descrittiva. Analizzeremo la media, la deviazione standard e visualizzeremo i dati tramite un istogramma e un box plot.
Inoltre, utilizzeremo il comando R density() che calcola la densità di probabilità stimata per i dati numerici contenuti in un vettore. E useremo la funzione plot() per graficare una curca di questa densità. In particolare, con il comando combinato **plot( density() )** che compare nel codice qui sotto, R calcola una curva che mostra graficamente dove i dati sono più densi (cioè dove ci sono più valori) e dove sono meno densi. Il grafico risultante mostrerà una curva liscia che rappresenta questa distribuzione.

# Creiamo un dataset di esempio con le altezze degli studenti.
altezza_studenti <- c(162 , 157 , 174 , 171 , 167 , 160 , 168 , 164 , 159 , 161 , 155 , 162 , 167 , 158 , 155 , 166 , 157 , 174 , 161 , 172 , 167 , 168 , 162 , 169 , 155 , 164 , 161 , 170 , 157 , 170 , 169 , 175 , 171 , 155 , 174 , 150 , 162 , 167 , 170 , 167 , 159 , 171 , 150 , 162 , 160 , 171 , 168 , 158 , 157 , 150 , 150 , 175 , 150 , 166 , 174 , 166 , 171 , 165 , 166 , 161 , 170 , 150 , 150 , 155 , 166 , 169 , 172 , 166 , 150 , 157 , 168 , 174 , 158 , 175 , 169 , 174 , 160 , 165 , 155 , 160) 

plot(density(altezza_studenti), ann=FALSE)	# comando che serve a visualizzare graficamente la distribuzione dei valori del vettore di dati di altezze in termini di densità di probabilità.
title(main="curva di densità stimata delle altezze", col.main="blue", xlab="altezze studenti osservate", ylab="Densità di Probabilità") 	 # aggiungo titolo al grafico e nome degli assi (che avevo lasciati bianchi nel comando sopra con l'opzione ann=FALSE)

#...**per te**: come commnteresti la curva che descrive i dati mostrata qui sopra? Ti suggerisce qualcosa?

#...**per te**: aggiungi una legenda in alto a destra nel plot che dica "altezze studenti"

# Calcolo della media
media_altezze <- mean(altezza_studenti)

# Calcolo della mediana
mediana_altezze <- median(altezza_studenti)

#...**per te**: aggiungi il valore di media e mediana come righe verticali nel plot creato qui sopra, rispettivamente come linee di colore "blue" e "orange". Per farlo, utilizza la funzione **abline()** incontrata negli esempi visti qui sopra.

#...**per te**: Crea un istogramma per visualizzare la distribuzione delle altezze.
#...**per te**: Crea un boxplot per visualizzare la distribuzione delle altezze.

WHAT’S NEXT

Ti stava piacendo e vorresti continuare a “giocare” con R?

Qui di seguito un paio di corsi di R gratuiti e disponibili online dall’ottimo progetto Software Carpentry (corsi in inglese):

Programming with R, disponibile qui: http://swcarpentry.github.io/r-novice-inflammation/

R for Reproducible Scientific Analysis, disponibile qui: http://swcarpentry.github.io/r-novice-gapminder/

E poi c’è la pagina dei manuali di R, ricchi di esempi ed esercizi, a vari livelli di difficoltà:

https://cran.r-project.org/manuals.html

Per lo più questi manuali sono disponibili in inglese, ma ne esistono anche alcuni in altre lingue, compreso l’italiano:

https://cran.r-project.org/other-docs.html#nenglish (scorri la pagina in basso per trovare i manuali disponibili in italiano)